[Deep Learning] 활성화 함수의 종류

내키는 대로 쓰는 글이라 두서가 없으며, 딥러닝 프레임워크에서 1줄 짜리 코드를 제공하기 때문에 샘플 코드 또한 없습니다.

 

2022.11.02 - [Deep Learning] - [Deep Learning] 활성화 함수

지난 글에서는 활성화 함수란 무엇이고 왜 사용하는가에 대해서 작성했습니다.

 

비선형성 확보를 위해 활성화 함수를 넣는다는 것은 알았으니 그럼 활성화 함수에는 어떤 종류가 있는지를 정리하려고 합니다.

 

---

 

순서는 다음과 같습니다.

• 시그모이드 함수 (Sigmoid function)
• 하이퍼볼릭 탄젠트 (tanh function)
• 소프트맥스 함수 (Softmax function)
• ReLU (ReLU function)

 

---

 

시그모이드 (Sigmoid function)

 

Figure 1. Sigmoid function

 

가장 먼저 살펴볼 것은 시그모이드 함수다. 함수는 위와 같이 생겼으며 수식은 다음과 같다.

 

$$ S(x) = \frac{1}{1 + e^{-x}} $$

 

위키백과에서는 시그모이드 함수를 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수라고 정의하고 있다.

 

특징

 

대표적으로 로지스틱 함수가 시그모이드 함수에 속하며 입력값을 (0,1)로 변환시킨다는 특성을 가지고 있다.

 

시그모이드 함수는 입력하는 값이 커질수록 1에 근접하며, 값이 작아질수록 0에 가까워진다. 이러한 특성으로 인해 시그모이드 함수는 확률을 구하는 문제에서 자주 사용된다.

 

단점

 

1. Gradient Vanishing 문제가 발생한다. 

 

Figure 2. Sigmoid function (derivative)

 

미분한 시그모이드 함수를 보면 함수의 최댓값이 0일 때 1/4인 것을 확인할 수 있고 입력 값이 올라갈수록 0으로 수렴한다. 이러한 특성 때문에 역전파시 아래 층에는 신호가 전달되지 않는 문제가 발생한다.

 

 

2. Non zero-centered

 

Figure 3. example of Sigmoid update

 

시그모이드 함수의 출력은 항상 양수이다. 이러한 특성 때문에 신경망의 가중치를 업데이트할 때 업데이트되는 가중치는 모두 양수이거나 모두 음수가 되고 그림 3과 같이 최적의 방향으로 업데이트 되지 못하고 1사분면과 3사분면 방향으로 업데이트 되면서 나아가는 편향 이동을 볼 수 있다.

 

결과적으로 이러한 특성은 신경망의 학습을 느리게 만든다.

 

 

3. 계산 비용

 

$$ S(x) = \frac{1}{1 + e^{-x}} $$

 

시그모이드 함수에 사용되는 exp 함수의 계산 비용이 크다는 단점이 존재한다.

 

 

---

 

하이퍼볼릭탄젠트  (Hyperbolic tangent function)

 

Figure 4. tanh function

 

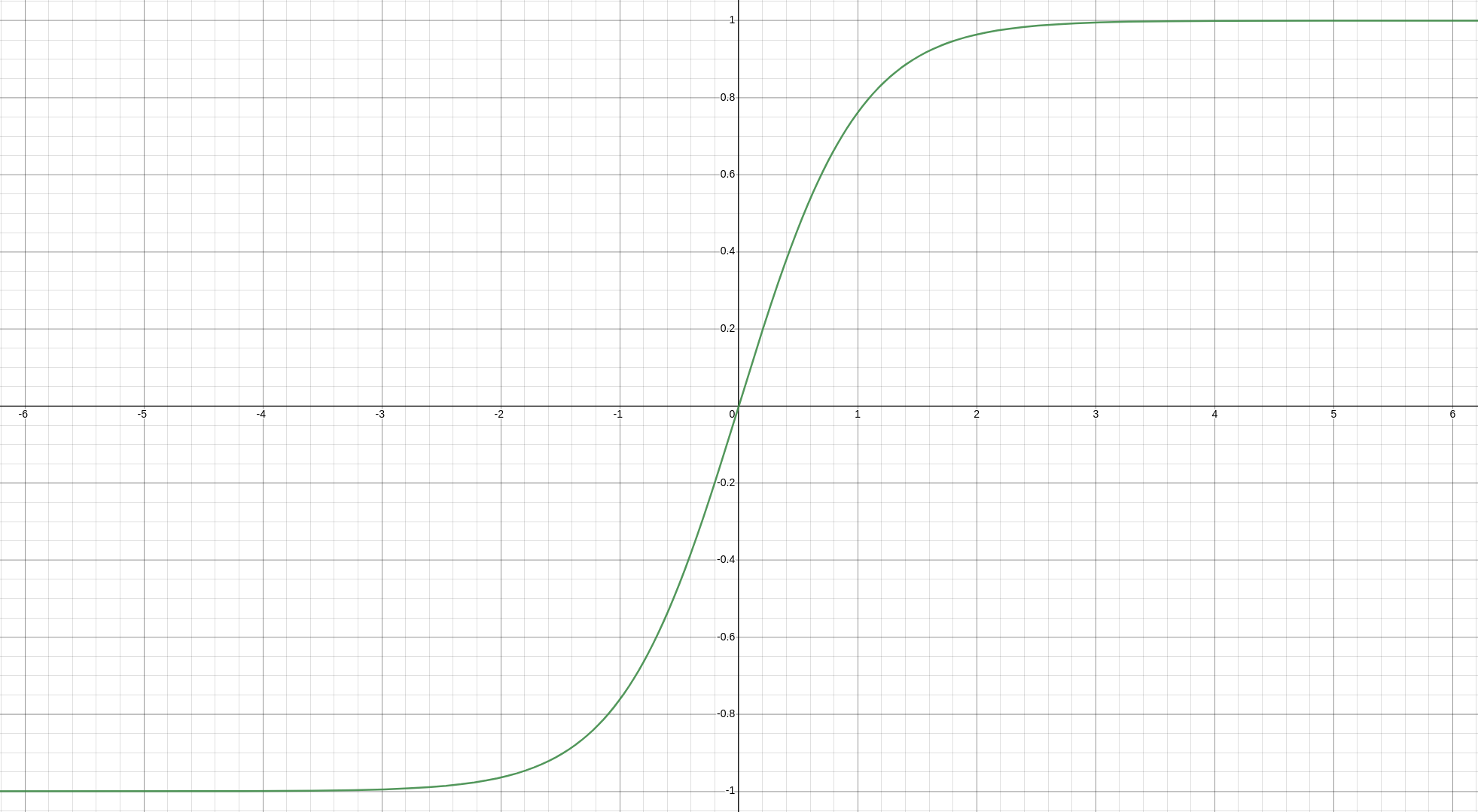
다음으로 살펴볼 tanh 함수는 위와 같이 생겼으며 함수의 수식은 다음과 같다.

 

$$ tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} $$

 

특징

 

tanh 함수는 입력된 값을 (-1, 1)로 변환시킨다.

 

입력되는 값이 클 수록 1에 가까운 값을 출력하고 입력 값이 작을수록 -1에 가까운 값을 출력한다. 이러한 특성으로 인해 시그모이드 함수에 비해 Gradient Vanishing이 적은 편이다.

 

또한 중심 값이 0이기 때문에 시그모이드 함수에서 non zero-centered로 인해 발생하던 편향 이동 또한 발생하지 않는다.

 

단점

 

1. Gradient Vanishing

 

시그모이드 함수에 비해 적어지기는 했지만 기울기 소실에 대한 문제는 여전히 남아있다.

 

---

 

소프트맥스 (Softmax function)

Figure 5. example of Softmax function

 

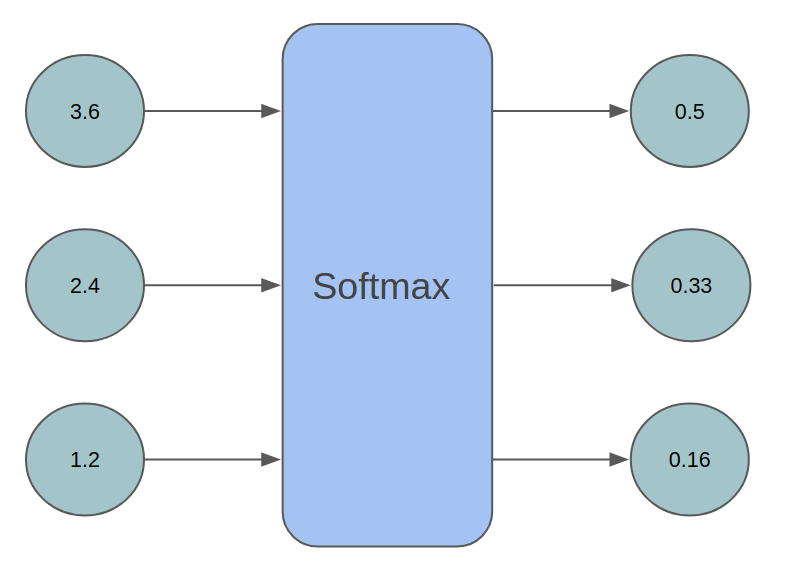
소프트맥스 함수의 수식은 다음과 같다.

 

$$ y_{k} = \frac{exp(a_{k})}{\sum_{i=1}^{n}exp(a_{i})} $$

 

특징

 

위키백과에서는 소프트맥스를 로지스틱 함수의 다차원 일반화라고 설명하고 있다.

 

소프트맥스는 다항 로지스틱 회귀에서 주로 쓰이며, n개의 입력을 받아서 n개의 결과를 출력하며 출력의 총 합이 1이라는 특성을 가지고 있다. 만약 입력이 1개라면 시그모이드 함수와 동일한 역할을 하게 된다.

 

이러한 특성으로 인해 주로 최종 레이어의 활성화 함수로 사용된다.

 

---

 

ReLU (Rectified Linear Unit)

 

Figure 6. ReLU function

 

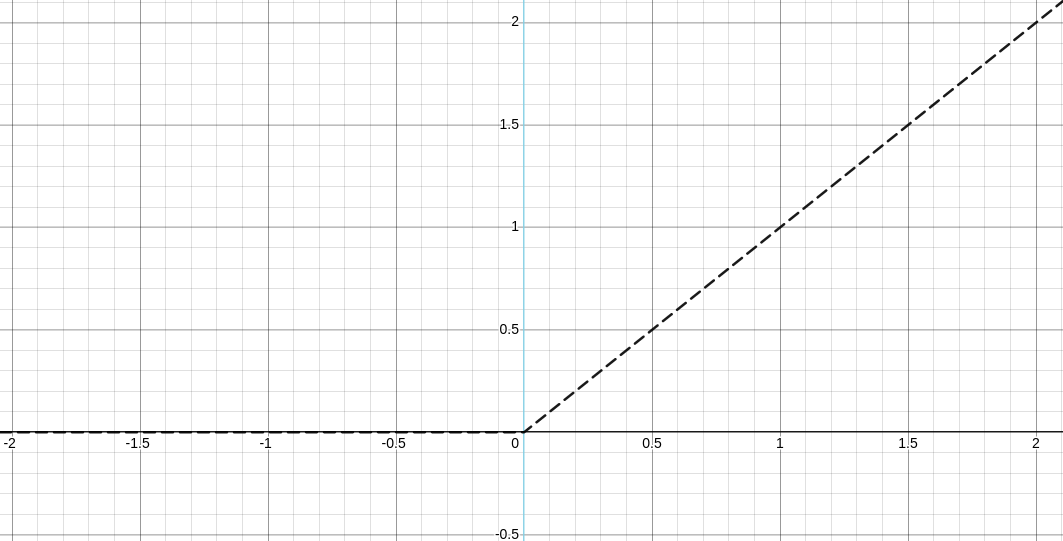
다음으로 살펴볼 함수는 가장 많이 사용되는 ReLU 함수이다. 수식은 다음과 같다.

 

$$ f(x) = max(0,x) $$

 

특징

 

ReLU 함수는 양수인 입력 값을 그대로 전달하기 때문에 신경망의 업데이트 중 가중치가 소실되는 문제가 발생하지 않으며, 구현이 간단하다는 특징을 가지고 있다.

 

또한 위와 같은 특징으로 인해 다른 활성화 함수에 비해 매우 빠른 학습속도를 보인다.

 

단점

 

1. Dead ReLU

Figure 7. Dead ReLU

 

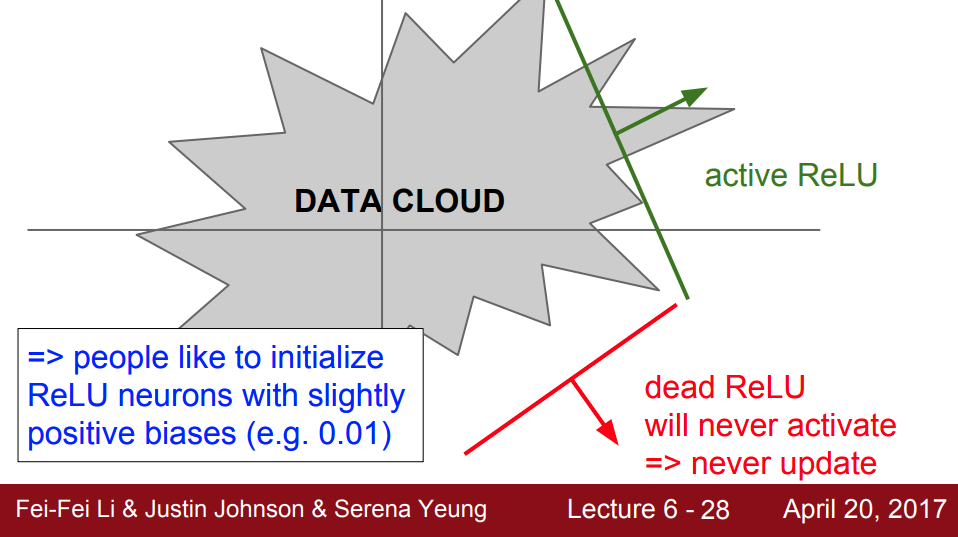
ReLU 함수는 입력 값이 음수일 경우 0을 출력하기 때문에 입력 값이 모두 음수일 경우 그림 7과 같이 가중치가 업데이트 되지 않는 Dead ReLU 또는 Dying ReLU라는 현상을 일으킨다.

 

이러한 현상으로 인해 보통 ReLU의 뉴런은 작은 값의 positive biases로 초기화한다.